For å sikre økonomisk forsvarlig utbygging og pålitelig drift av både nye og eksisterende anlegg er det helt nødvendig å dimensjonere kabelanleggene optimalt. Strømføringsevnen til en kraftkabel (også kalt overføringskapasiteten eller belastningsevnen) er begrenset av oppvarming fra den elektriske strømmen og dimensjoneres etter temperaturen kabelen tåler.
I denne teksten kan du lese om flere av de viktigste faktorene som er viktig å ta høyde for ved dimensjonering av kabelanlegg, og du får en oversikt over de forskjellige måtene belastningsevnen kan regnes ut. SINTEF har solid kompetanse innen beregning og vurdering av strømføringsevne og har gjennomført flere forskningsprosjekter og direkteprosjekter.

Les mer:
- SINTEFs kompetanse innen elkraftkomponenter
- Kabelskjermer: hva er problemene og hvordan skal de løses?
- Elektriske kontakter – en vanlig årsak til havari og branner
- Sensorer for å bestemme strømføringsevnen til kraftkabler
- Massene rundt kraftkablene: en viktig bidragsyter til strømføringsevnen
Kabeldesign
En moderne kraftkabel er et høyteknologisk produkt med høy pålitelighet og lang levetid. Kablene er et resultat av avansert material-, konstruksjons- og produksjonsteknikk, og består grovt sett av leder, isolasjon, metallskjerm og ytterkappe. Strømmen går gjennom den metalliske lederen, som regel aluminium eller kobber. På grunn av spenningen (typisk opptil 420 kV) er lederen isolert med svært rent kryssbundet polyetylen (PEX/XLPE) som tåler høye elektriske felt. Utenpå isolasjonen ligger et nytt metall-lag i form av aluminiumslaminat og/eller kobbertråder som fører jordstrømmer. Ytterst ligger et beskyttende lag med polyetylen (PE). Sjøkabler har også et ytre lag med armering av jern eller kobber for ekstra mekanisk beskyttelse.

Både lederen, metallskjermer og eventuell armering eller metallrør utvikler varme når kabelen fører strøm. For høyere spenningsnivå (typisk ≥ 245 kV) er det også varmeutvikling i isolasjonen forårsaket av ladestrømmen, kalt dielektriske tap.
Varmeutvikling i lederen er i hovedsak bestemt av laststrømmen (typisk inntil 2500 A), tverrsnitt (typisk inntil 2500 mm2), ledermateriale (aluminium eller kobber), frekvens (DC eller 50 Hz AC) og ledertype (kompakt, flertrådede, segmentert eller milliken). I kraftkabler som fører vekselstrømmer vil ikke strømmen fordele seg jevnt i lederen, men strømtettheten vil være størst i overflaten. For anlegg med svært høye strømmer, for eksempel fra i vannkraftverk, blir skinner eller hule rør brukt for å redusere tapene på grunn av dette.

Varmeutvikling i metallskjermer avhenger av hvordan skjermene er koblet (ensidig eller tosidig), laststrøm, tverrsnitt, materiale og skjermtype (laminat eller tråder).
Varmeutvikling i armering avhenger av mange av de samme faktorene som metallskjermer. En forskjell er at armeringen kan være laget i magnetisk materiale som er utfordrende å regne nøyaktig på. I mange tiår er det forsket på forskjellige modeller for å kunne regne korrekt på tap i armeringene, samtidig som dens påvirkning på lagene innenfor (leder og skjerm) inkluderes på en god måte.

Forlegning/installasjon
Hvordan en kabel legges eller installeres i bakken har stor påvirkning på strømføringsevnen. Det er ofte variasjoner i forlegningen langs en trasé, og detaljert informasjon kan ofte være ukjent eller usikker. For en enkel grøft trengs som et minimum:
- kabeltype,
- forlegningsdybde (ofte 0.5-1.0 m),
- de termiske egenskapene til kabelsand (termisk resistivitet: ofte 1 m*K/W og varmekapasitet: ofte 2.0 MJ/(m3∙K),
- omgivelsestemperatur (ofte 15°C)
- forlegning (trekant eller flat)
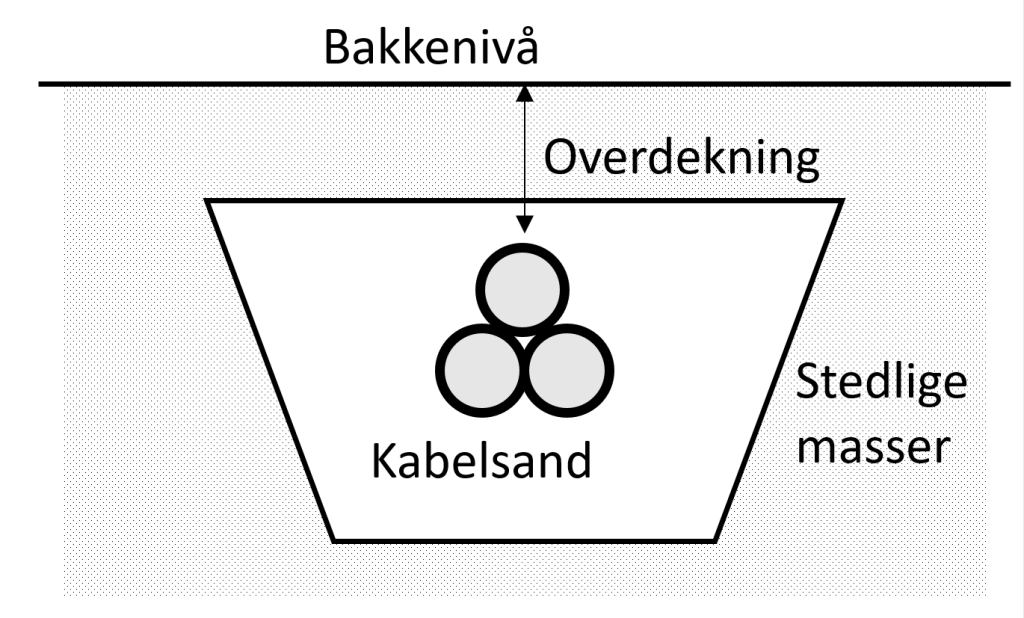
Andre forhold kan være:
- andre parallelle kabelgrupper,
- krysninger av andre kabler,
- fjernvarmerør,
- forlegning i rør, betongkanaler (OPI), kulvert eller under vei,
- forlegning innendørs (som i nettstasjoner)
- kjøling, enten aktiv eller passiv kjøling, vann eller luft

Beregninger – analytisk
Det er gjennom internasjonalt samarbeid blitt utarbeidet dimensjoneringsmetoder for kabler. Dette arbeidet er standardisert i IEC 60287 og består av to hoveddeler: metoder for å bestemme effektutvikling, og metoder for å bestemme termiske motstand. Beregninger med IEC 60287 er basert på en kombinasjon av analytiske formler og forenklede empiriske uttrykk som beskriver varmeutvikling og varmespredning for de fleste kabeltyper og relevante grøfter og geometrier. Formelverket baserer seg på beregningsmetoder som antar at kabelen har nådd stasjonær-temperatur etter lang tid i kontinuerlig drift. For dette driftsmønsteret trengs det bare å tas hensyn til varmen som utvikles i systemet, termiske mostander og omgivelsestemperatur. Da får man følgende formel hvor konstantene er oppgitt i standarden for forskjellige kabler og grøfter:
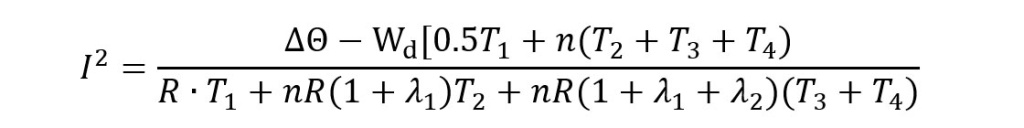
I er strømpåtrykk i leder, θ differanse mellom ledertemperatur og omgivelsestemperatur, Wd dielektriske tap, n antall ledere, T1 termisk resistans mellom leder og skjerm, T2 termisk resistans mellom skjerm og armering, T3 termisk resistans i ytterkapper, T4 termisk resistans i omgivelser, R AC-motstand til leder, λ1 andel av totaltapene i metallskjermer λ2 andel av totaltapene i armering.
Å lage modeller basert på formelverket er tidskrevende, spesielt for anlegg med mange kabler. Kabelleverandørene har over mange tiår opparbeidet egne programmer basert på eksisterende formelverk. Det finnes også kommersielt tilgjengelige programvarer. I tillegg til IEC 60287 finnes supplerende formelverk for blant annet å regne på tidsvarierende last og forlegning i ugunstige termiske miljø.
Beregninger – tabellverdier
For enklere anlegg er det laget tabellverdier basert på IEC 60287. I Norge har ofte NEN 62.75 vært benyttet, eller tabeller som leverandørene selv oppgir i datablad. Tabellverdiene oppgir belastning for en standardforlegning med én kabelkrets som forlegges i tett trekant eller flatt, typisk forlegningsdybde på 50-70 cm og omgivelsestemperatur på 15°C. Dersom en kabelforlegning avviker fra en standardforlegning i tabellene (antall kabler, rør, forlegningsdybde etc.) må det benyttes tabellverdier for reduksjonsfaktorer (også kalt korreksjonsfaktorer).
Tabellverdiene vil i mange tilfeller ikke gi fleksibiliteten som er nødvendig for å gjøre tilstrekkelig strømføringsevneberegninger for dagens kabelanlegg. Dette er spesielt viktig i de termiske flaskehalsene, som ofte hele anlegget dimensjoneres for, ettersom de er mer kompliserte eller annerledes enn standardutvalget som oppgis. Resultatet er ofte at strømføringsevnen beregnes for høyt, for lavt eller at flaskehalser regelrett neglisjeres. Alle scenarioene gir en usikkerhet til den faktiske strømføringsevnen. Resultatet kan enten føre til at det er ubrukt kapasitet i nettet, eller øke risikoen for lokal overoppheting og havari.
Beregninger – numerisk
Beregning av strømføringsevne med endelig element-analyse/metoden (finite element analysis/method – FEA/FEM) blir stadig mer populært, ikke bare i forskningsmiljøer, men også blant konsulenter og hos kabelleverandører. FEA er en metode som løser differensialligninger numerisk og hvor problemet (kabelen og omliggende masser) deler inn i mindre elementer (mesh).

En fordel er at man står nærmest fritt til å regne på alle mulige kabler og forlegninger. Det finnes flere gode instruksjonsvideoer og oppgaver for nybegynnere, men det er tidkrevende å sette seg inn i programvaren og fysikken.
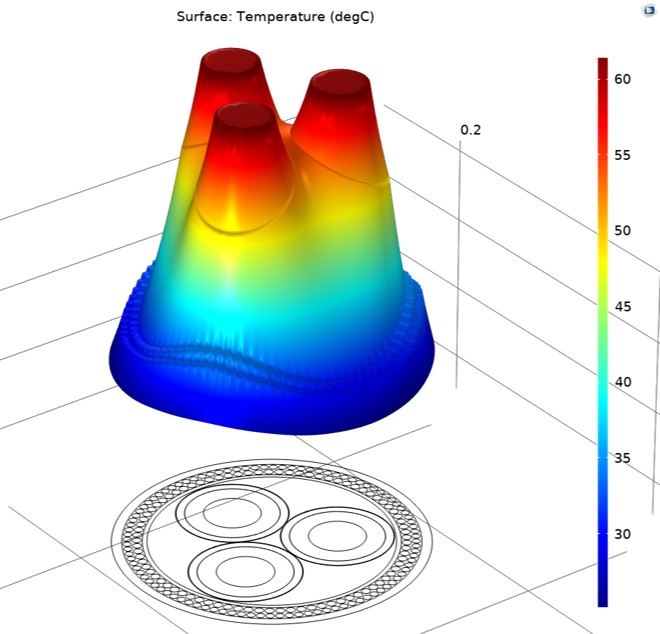
For de enkleste beregningene må fysikkene for magnetfelt og varmeledning inkluderes. For mer avanserte forlegninger kan det være nødvendig å inkludere stråling og konveksjon (strømning), hvor ligningene for den siste er ulineære. Dette kan fort ende opp med modeller som kan være tidkrevende å løse, om de i det hele tatt lar seg løse.
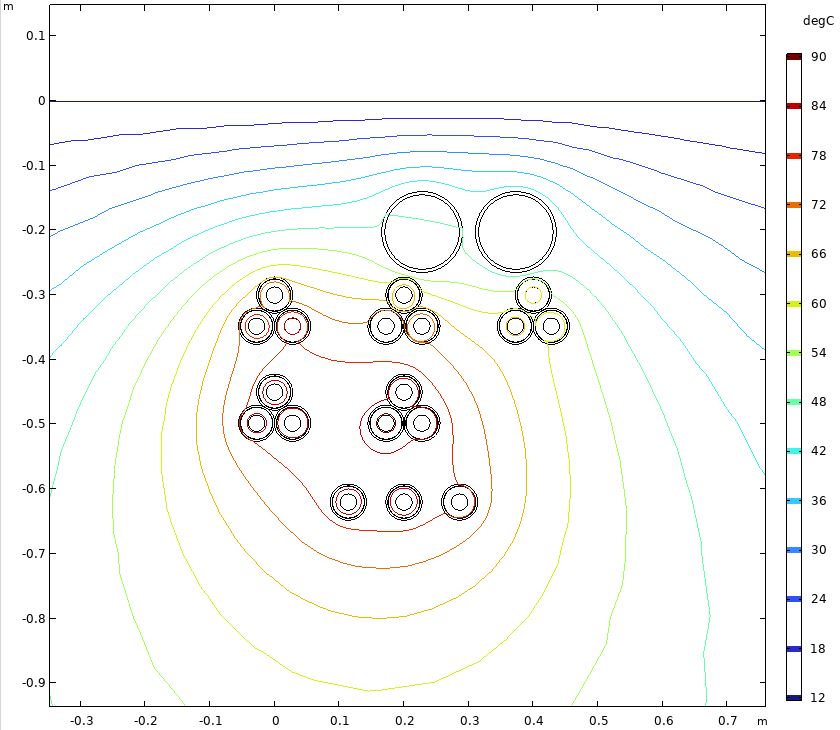
Også FEA har sine begrensninger. Å regne på grøftesnitt med vanlige kabler forlagt i bakke er relativt kurant når man har lært seg programvaren. Beregningene gjøres vanligvis i 2D, som antar at seksjonen er tilstrekkelig lang så det ikke er noen endeeffekter, helst over 6 meter. Dersom flaskehalsen er en kort strekning hvor aksiell varmeledning er av betydning (ofte fra 0.5 til 3 meter), eller det er kryssende linjer, må beregningene gjøres i 3D, som er kompliserende. Det øker behovet for minne og datakraft betraktelig.
Driftsmønster
Kablene dimensjoneres som regel for kontinuerlig last, noe som ofte ikke er det reelle driftsmønsteret. Siden mange kabelanlegg bare i kortere perioder har høy last er det mye uutnyttet kapasitet. Driftsmønster i forskjellige anlegg kan variere mye avhengig av forbruker; fra husholdninger med (historisk sett) høyt forbruk morgen og ettermiddag i ukedagene, til industrikunder som kan ha jevn belastning over lang tid. Driftsmønsteret for kabler tilknyttet vindkraft vil variere fra time til time og dag til dag etter vindforholdene, mens kabler til ladeanlegg for elbiler og ferjer kan ha et mer repetitivt (men dynamisk) belastningsmønster.
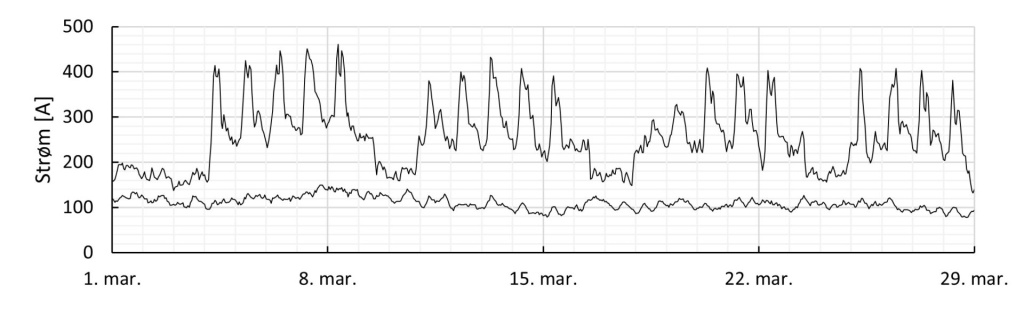
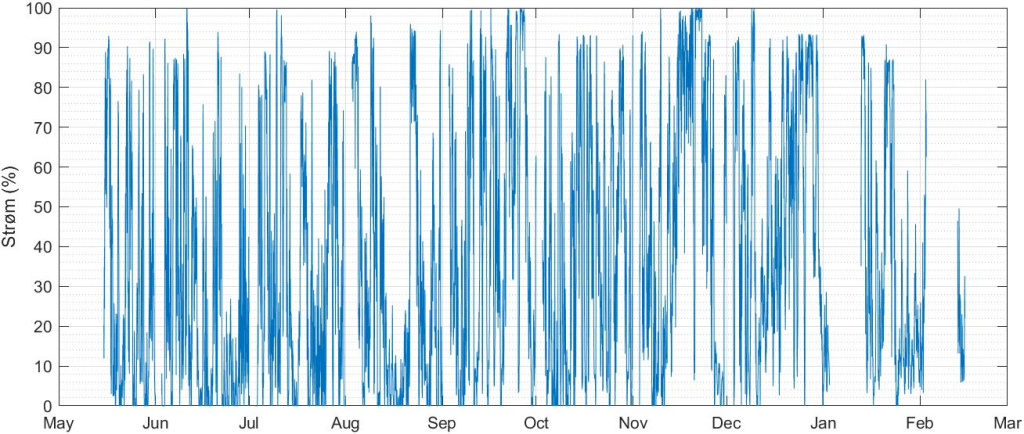
Å dimensjonere for varierende last kan øke kompleksiteten betydelig avhengig av detaljnivå. En gjennomførbar metode er å dimensjonere etter en lastfaktor (I0) fremfor høyeste kontinuerlige strøm (Imax). Lastfaktoren er gjennomsnittslast over en periode, dividert på maksimallast i samme perioden. Dette må fås fra systemplanleggere (nye anlegg) eller fra målte lastdata (eksisterende anlegg). For en 24-timers periode får man da formelen under, hvor Ii er gjennomsnittlig timeslast:
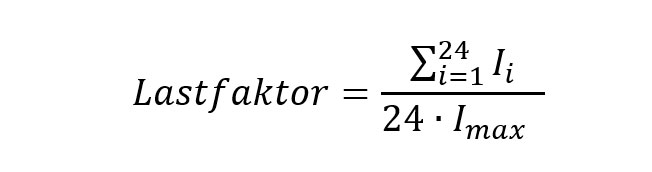
For beregning av strømføringsevne er det varmeutvikling, ikke strømmen i seg selv som må hensyntas. Varmeutvikling (P) er proporsjonale med strømmen kvadrert (P=R∙I2), hvor R er resistans. Ved å bruke denne sammenhengen fås en tapfaktor (µ):
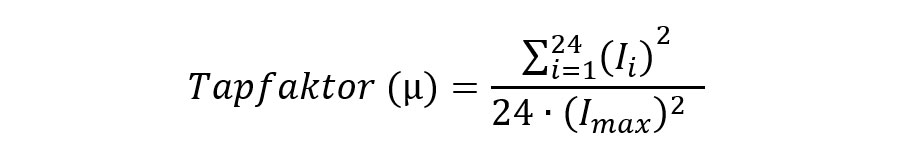
I sin enkleste form kan kabelen dimensjoneres etter I0=√µ∙Imax, fremfor bare Imax. Denne sammenhengen må imidlertid brukes med forsiktighet, ettersom den ikke tar hensyn til viktige aspekter som størrelsen på kablene og termiske tidskonstanter. For eksempel vil kabler forlagt i luft eller i rør ha kortere tidskonstanter enn kabler i grøft, som fører til raskere oppvarming og nedkjøling. Det finnes flere betraktninger, som i CIGRE-brosjyren TB640 og i standarden IEC 60853. I disse brukes mellom annet en syklisk faktor (M) hvor √µ inngår som en enkelt parameter i en større ligning. Kablene dimensjoneres da for I0=M∙Imax.
Oppsummering
Å beregne strømføringsevne er viktig for å vite kapasiteten i nye og eksisterende anlegg. For enkle anlegg kan det være tilstrekkelig med tabellverdier, mens dedikert programvare (analytisk eller numerisk) ofte er nødvendig for mer avanserte. Informasjon om selve kraftkabelen og forlegningen langs hele trasèen er essensielt for å regne mest mulig nøyaktig. SINTEF har flere tiårs erfaring med beregninger og målinger fra både forskningsprosjekter og direkteprosjekter.










Kommentarer
Hei Ivar Magnus. Takk for flott tilbakemelding! Det manglet en kvadratrot i uttrykket, det er nå rettet opp. Har også lagt inn en presisering om at dette er den enkleste måten å bruke tapsfaktor på (må brukes med forsiktighet), men at det er er flere mer detaljerte og mer nøyaktige metoder, som for eksempel en syklisk faktor («cyclic rating factor») M.
Noen gode steder for videre fordypning:
• CIGRE TB640, seksjon 5.1.2,
• IEC 60853-1 (til og med 36 kV) og IEC 60853-2 (over 36 kV)
• «Rating of electric power cables: ampacity computations for transmission, distribution, and industrial applications», George J Anders 1997, seksjon 5.6.2
Lurer på om det mangler en kvadratrot i uttrykket og at uttrykket egentlig blir Io=√μ*Imax. Dersom uttrykket nederst i artikkelen stemmer vil en for en hsp. avgang som beregnes til 270 A 90 grader Celsius kunne laste den med 375 A i topptimen ved en typisk døgnprofil. Dersom en bruker kvadratroten av uttrykket for μ vil en med samme døgnprofil kunne laste kabelen med 317 A i maxtimen. Gir mer mening for meg at lastfaktoren er lavere enn tapsfaktoren i og med at ved et kvadratisk uttrykk vil timene med høy strøm gi mer termisk bidrag enn timene med lav strøm. Lurer på om dere kan se på dette 🙂